I asked a question about stereochemistry http://wwmm.ch.cam.ac.uk/blogs/murrayrust/?p=2643 and owe the community an answer. The answer is my answer. It may or may not be “right”. I don’t like the word “right” in science. But I hope it’s acceptable to those who think about the problem. I showed two pictures
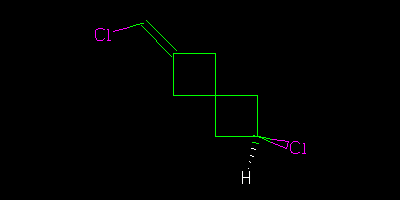
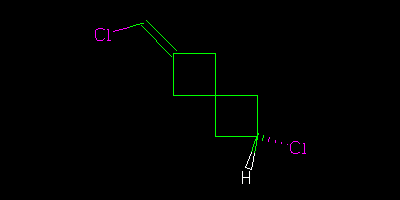
And asked what the relationship of these molecules was. The “right” answer was to be that it was impossible to tell as there is a stereocentre in the middle of the molecule that is undefined. But it was suggested that because the two molecules were drawn in the same way then we might (not “should” but “could”) assume that the stereocentre was consistent. In which case we could say that although we didn’t know what the molecules actually were we could say they were geometrical isomers, not enantiomers.
If I had drawn all the centres explicitly
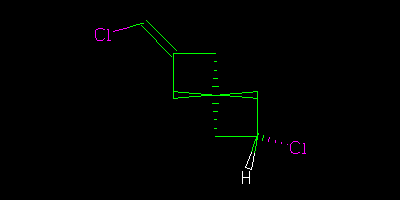
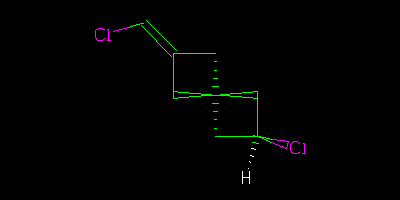
Then we could say “definitely” that the two were geometrical isomers (cis/trans, configuration, … I am using http://en.wikipedia.org/wiki/Cis%E2%80%93trans_isomerism terminology).
There’s an assumption that conformation doesn’t play a role – that the cyclobutane ring flips rapidly enough to “average” the structure. Here’s Wikipedia’s example of cyclohexanes:
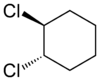
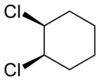
Alicyclic compounds can also display cis-trans isomerism. As an example of a geometric isomer due to a ring structure, consider 1,2-dichlorocyclohexane:
Note that the cis- compound as drawn can have enantiomers. What we all “know” is that at room temperature they intercovert so that the molecule is not optically active. But if we cool it down or look at a very short time scale then it would, indeed have enantiomers. So we have to be very careful in how we phrase the questions because people make assumptions. And my assumption is often not your assumption.
==== Next divertissement ====
I am now writing parsers for compchem log files. This engages some of the pleasure/hate centres of my brain in the same way as Sudoku does – and it’s slightly more productive. Here’s a typical bit of a log file. It doesn’t matter what the numbers are or what they mean
…. . . . omitted . . .
28 H 2.700772 3.229400 5.731856 4.467482 7.448261
29 H 1.099958 2.072781 5.129949 3.144928 5.344895
30 H 1.920507 0.965845 5.216951 4.614282 6.231286
21 22 23 24 25
21 H 0.000000
22 H 1.777203 0.000000
23 H 5.002806 5.524624 0.000000
24 H 6.096661 6.315358 1.774278 0.000000
25 H 7.214158 8.252435 4.711394 4.561542 0.000000
26 H 8.228138 9.136704 6.730950 6.277461 2.501917
27 H 7.915186 8.417597 7.182659 6.464504 4.302447
28 H 6.508693 6.586577 5.931001 5.094904 4.950885
29 H 4.817286 4.590808 4.296008 3.705276 5.455187
30 H 6.292404 5.863642 3.978192 2.711028 6.081788
. . .Snipped.. .
Question: (a) what would be the next line – precisely – and (b) what would the line after that start with?
And how would you write a parser for it
Looks to me like this is a distance matrix, so the next line would be
26 27 28 29 30
and the line following that would be
26 H X.XXXXXX
But this could be a hessian matrix too – or really any (symmetric) matrix NxN, where N=number of atoms.
Well done. How might you tell between a distance matrix and a Hessian?
The hessian might have negative values – the distance matrix would never have negative values. The hessian might have quite a few values that were near zero – the distance matrix would never have near zero values.
Excellent reasoning.
And do the diagonal values tell you anything?
Well, that’s perhaps THE way to distinguished the distance matrix from the Hessian matrix. The diagonal elements of the distance matrix are all zero; in fact one typically does not even print out the diagonal elements for this reason. The Hessian diagonal elements are likely non-zero. If the Hessian is diagonalized, then the diagonal elements are the force constants – 6 will be essentially zero, the rest are all positive if you have a local energy minimum, one will be negative if you have a TS, etc.